
Note:
All questions are compulsory. Marks are allotted in front of each question.
Write your Name, Enrolment Number, Study Centre Name and Subject on the top of the first page of the answer sheet
1.Answer any one out of the following questio
Write the following sets in roster form 2
(a) A = {x : x is an integer and –3 ≤ x < 7}
Answer-
\[ A = \{x \mid x \text{ is an integer and } -3 \leq x < 7\} \]
In roster form:
\[ A = \{-3, -2, -1, 0, 1, 2, 3, 4, 5, 6\} \]
b)B = {x : x is a natural number less than 6}
Answer-
The set \( B \) can be represented in roster form as follows:
\[ B = \{1, 2, 3, 4, 5\} \]
This set includes all natural numbers less than 6, specifically 1, 2, 3, 4, and 5.
Or
(a)From the given figure, find tan P – cot R.
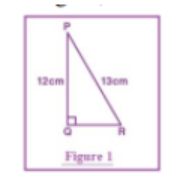
Answer-
In the right triangle \( PQR \) with sides \( PQ = 12 \), \( PR = 13 \), and \( QR = 5 \), we can use the trigonometric ratios to find \( \tan P \) and \( \cot R \), and then calculate \( \tan P – \cot R \).
First, find \( \tan P \):
\[ \tan P = \frac{{\text{Opposite side (QR)}}}{{\text{Adjacent side (PQ)}}} = \frac{5}{12} \]
Next, find \( \cot R \):
\[ \cot R = \frac{1}{{\tan R}} \]
We previously found \( \tan R = \frac{12}{5} \). Substitute this value:
\[ \cot R = \frac{1}{{\frac{12}{5}}} = \frac{5}{12} \]
Now, calculate \( \tan P – \cot R \):
\[ \tan P – \cot R = \frac{5}{12} – \frac{5}{12} \]
Combine the numerators:
\[ \tan P – \cot R = \frac{0}{12} \]
Simplify the fraction:
\[ \tan P – \cot R = 0 \]
Therefore, \( \tan P – \cot R = 0 \) in the given triangle.
b. Prove that (sin4θ−cos4θ+1)cosec2θ=2
Answer–
\[ \text{L.H.S.} = (\sin^4\theta – \cos^4\theta + 1) \cosec^2\theta \]
\[ = [(\sin^2\theta – \cos^2\theta)(\sin^2\theta + \cos^2\theta) + 1] \cosec^2\theta \]
\[ = (\sin^2\theta – \cos^2\theta + 1) \cosec^2\theta \, \text{[Because } \sin^2\theta + \cos^2\theta = 1\]
\[ = 2\sin^2\theta \cosec^2\theta \, \text{[Because } 1 – \cos^2\theta = \sin^2\theta\]
\[ = 2 \]
\[ \text{RHS} = 2 \]
\[ \text{L.H.S.} = \text{RHS} \]
2.Answer any one out of the following questions.
(a) Find the 28th term from the end of the AP 6, 9, 12, 15, 18, ..…, 102.
Answer–
The common difference (\(d\)) in the arithmetic progression is calculated as follows:
\[ d = a_{n} – a_{n-1} \]
Substitute the given values:
\[ d = 9 – 6 = 3 \]
Now, use the formula to find the \(n\)th term (\(a_n\)) of an arithmetic progression:
\[ a_n = a + (n-1)d \]
Substitute the values \(a = 6\), \(d = 3\), and \(n = 28\) into the formula:
\[ a_{28} = 6 + (28-1) \times 3 \]
\[ a_{28} = 6 + 27 \times 3 \]
\[ a_{28} = 6 + 81 \]
\[ a_{28} = 87 \]
Therefore, the 28th term from the end of the arithmetic progression \(6, 9, 12, 15, 18, \ldots, 102\) is 87.
b) How many 3-digits numbers are divisible by 7?
Answer–
The first 3-digit number divisible by 7 is 105, and the last 3-digit number divisible by 7 is 999. To find how many 3-digit numbers are divisible by 7, we can use the formula for finding the number of integers in an arithmetic sequence.
The formula is given by:
\[ \text{Number of terms} = \frac{\text{Last term} – \text{First term}}{\text{Common difference}} + 1 \]
In this case:
\[ \text{Number of terms} = \frac{999 – 105}{7} + 1 \]
\[ \text{Number of terms} = \frac{894}{7} + 1 \]
\[ \text{Number of terms} = 127 + 1 \]
\[ \text{Number of terms} = 128 \]
Therefore, there are 128 three-digit numbers divisible by 7.
OR
(a) The sum of some terms of a GP is 315. Its first term is 5 and the common ratio is 2. Find the number of its terms and the last term.
Answer–
The formula for the sum (\(S_n\)) of the first \(n\) terms of a geometric progression (GP) is given by:
\[ S_n = \frac{{a \cdot (r^n – 1)}}{{r – 1}} \]
where:
– \(a\) is the first term,
– \(r\) is the common ratio,
– \(n\) is the number of terms.
Given that \(S_n = 315\), \(a = 5\), and \(r = 2\), we can substitute these values into the formula and solve for \(n\):
\[ 315 = \frac{{5 \cdot (2^n – 1)}}{{2 – 1}} \]
Simplify the equation:
\[ 315 = 5 \cdot (2^n – 1) \]
Divide both sides by 5:
\[ 63 = 2^n – 1 \]
Add 1 to both sides:
\[ 64 = 2^n \]
Taking the logarithm base 2 of both sides:
\[ n = \log_2(64) \]
\[ n = 6 \]
Therefore, the number of terms (\(n\)) in the geometric progression is 6.
To find the last term (\(L\)), we can use the formula for the nth term in a GP:
\[ L = a \cdot r^{(n-1)} \]
Substituting the given values:
\[ L = 5 \cdot 2^{(6-1)} \]
\[ L = 5 \cdot 2^5 \]
\[ L = 5 \cdot 32 \]
\[ L = 160 \]
Therefore, the number of terms is 6, and the last term is 160.
(b) Find the common ratio of a GP whose sum of infinite terms is 8 and its second term is 2.
Answer–
The sum (\(S_\infty\)) of an infinite geometric progression (GP) is given by the formula:
\[ S_\infty = \frac{a}{1 – r} \]
where:
– \(a\) is the first term,
– \(r\) is the common ratio.
Given that \(S_\infty = 8\), we can express this in the form:
\[ 8 = \frac{a}{1 – r} \]
Now, we are also given that the second term (\(a_2\)) is 2. The second term of a geometric progression is given by:
\[ a_2 = a \cdot r \]
In this case:
\[ 2 = a \cdot r \]
Now, we have a system of two equations:
\[ 8 = \frac{a}{1 – r} \]
\[ 2 = a \cdot r \]
Let’s solve this system. First, rearrange the second equation to express \(a\) in terms of \(r\):
\[ a = \frac{2}{r} \]
Now, substitute this expression for \(a\) into the first equation:
\[ 8 = \frac{\frac{2}{r}}{1 – r} \]
To simplify, cross-multiply:
\[ 8(1 – r) = 2r \]
Expand and rearrange the equation:
\[ 8 – 8r = 2r \]
\[ 10r = 8 \]
\[ r = \frac{4}{5} \]
Therefore, the common ratio (\(r\)) of the geometric progression is \(\frac{4}{5}\).
3 Answer any one out of the following questions.
a) If z1 = 2 + 8i and z2 = 1 – i, then find |z1/z2|.
Answer–
Given \( z_1 = 2 + 8i \) and \( z_2 = 1 – i \), the expression to find is \( \left|\frac{z_1}{z_2}\right| \).
To find \( \frac{z_1}{z_2} \), multiply \( z_1 \) by the conjugate of \( z_2 \):
\[ \frac{z_1}{z_2} = \frac{2 + 8i}{1 – i} \times \frac{1 + i}{1 + i} \]
After simplifying, we get \( \frac{z_1}{z_2} = -3 + 5i \).
Now, find the modulus \( |z_1/z_2| \):
\[ \left|\frac{z_1}{z_2}\right| = \sqrt{(-3)^2 + (5)^2} \]
\[ \left|\frac{z_1}{z_2}\right| = \sqrt{9 + 25} \]
\[ \left|\frac{z_1}{z_2}\right| = \sqrt{34} \]
Therefore, \( \left|\frac{z_1}{z_2}\right| = \sqrt{34} \).
b) Suppose z = (2 – i)2 + [(7 – 4i)/(2 + i)] – 8, express z in the form of x + iy such that x and y are real numbers.
Answer– Let’s simplify the expression z step by step:
\[ z = 2(2 – i) + \frac{7 – 4i}{2 + i} – 8 \]
\[ z = 4 – 2i + \frac{(7 – 4i)(2 – i)}{5} – 8 \]
\[ z = 4 – 2i + \frac{14 – 15i – 8i + 4i^2}{5} – 8 \]
\[ z = 4 – 2i + \frac{18 – 23i}{5} – 8 \]
\[ z = 4 – 2i + \frac{18}{5} – \frac{23i}{5} – 8 \]
Combine the real and imaginary parts:
\[ z = \frac{14}{5} – \frac{33i}{5} \]
Therefore, \( z = \frac{14}{5} – \frac{33i}{5} \) in the form \( x + iy \) where \( x = \frac{14}{5} \) and \( y = -\frac{33}{5} \).
OR
a) Solve the inequality x2 + x – 28 < 2.
Answer–
\[x^2 + x – 28 < 2\]
Rearrange the inequality:
\[x^2 + x – 28 – 2 < 0\]
Combine like terms:
\[x^2 + x – 30 < 0\]
Factor the quadratic expression:
\[(x – 5)(x + 6) < 0\]
Now, identify the intervals where this expression is negative. The critical points are where \(x – 5 = 0\) (i.e., \(x = 5\)) and \(x + 6 = 0\) (i.e., \(x = -6\)).
Create intervals using these critical points:
\[(-\infty, -6) \cup (-6, 5) \cup (5, \infty)\]
Now, test a value in each interval to determine the sign of the expression:
– For \(x = -7\): \((-\infty, -6)\) \(\implies\) \((-7 – 5)(-7 + 6) < 0\) \(\implies\) \(12 > 0\), which is true.
– For \(x = 0\): \((-6, 5)\) \(\implies\) \((0 – 5)(0 + 6) < 0\) \(\implies\) \(-30 < 0\), which is true.
– For \(x = 6\): \((5, \infty)\) \(\implies\) \((6 – 5)(6 + 6) < 0\) \(\implies\) \(66 > 0\), which is true.
Since the inequality is satisfied in the intervals \((-6, 5)\), the solution to \(x^2 + x – 28 < 2\) is \(x \in (-6, 5)\).
4. Answer any one out of the following questions
a) In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Answer
The word MISSISSIPPI consists of one M, four I’s, four S’s, two P’s, and a total of 11 letters.
To determine the total number of possible arrangements with these letters, consider the permutations of all the letters, which is expressed as \( \frac{11!}{1! \cdot 4! \cdot 4! \cdot 2!} \).
Now, focus on the case when all the I’s are grouped together. This forms one M, one unit of four I’s, four S’s, two P’s, resulting in a total of 8 units. The number of arrangements in this case is given by \( \frac{8!}{1! \cdot 4! \cdot 4! \cdot 2!} \).
Therefore, the distinct permutations of the letters of the word MISSISSIPPI when the four I’s do not come together is found by subtracting the arrangements when I’s are together from the total arrangements: \( \frac{11!}{1! \cdot 4! \cdot 4! \cdot 2!} – \frac{8!}{1! \cdot 4! \cdot 4! \cdot 2!} = 34650 – 840 = 33810 \).
b) How many 5-digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once?
Answer–
To determine the number of 5-digit telephone numbers that can be constructed using the digits 0 to 9, with the condition that each number starts with 67 and no digit appears more than once, we can use the permutation formula.
The formula for permutations of \(r\) distinct items taken from a set of \(n\) distinct items is given by:
\[ P(n, r) = \frac{n!}{(n-r)!} \]
In this case, since each number starts with 67, we have already used two digits. Therefore, we need to choose 3 more digits from the remaining 8 digits (0 to 9 excluding 6 and 7) to form a 5-digit number.
\[ P(8, 3) = \frac{8!}{(8-3)!} \]
\[ P(8, 3) = \frac{8!}{5!} \]
Now, calculate the permutations:
\[ P(8, 3) = \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times 1} \]
\[ P(8, 3) = 8 \times 7 \times 6 \]
\[ P(8, 3) = 336 \]
Therefore, there are 336 different 5-digit telephone numbers that can be constructed using the digits 0 to 9, with each number starting with 67 and no digit appearing more than once.
OR
a) A committee of 3 persons is to be constituted from a group of 2 men and 3 women. In how many ways can this be done? How many of these committees would consist of 1 man and 2 women?
Answer–
The number of ways to form a committee of 3 persons from a group of 2 men and 3 women is given by the combination formula:
\[ C(n, r) = \frac{n!}{r!(n-r)!} \]
where \( n \) is the total number of people, \( r \) is the number of people to be selected, and \( ! \) denotes factorial.
Forming a Committee of 3 Persons:
\[ C(5, 3) = \frac{5!}{3!(5-3)!} \]
\[ C(5, 3) = \frac{5!}{3! \cdot 2!} \]
\[ C(5, 3) = \frac{5 \cdot 4}{2} \]
\[ C(5, 3) = 10 \]
So, there are 10 ways to form a committee of 3 persons from the group. Forming a Committee with 1 Man and 2 Women:
To form a committee with 1 man and 2 women, we choose 1 man out of 2 and 2 women out of 3:
\[ C(2, 1) \times C(3, 2) = \frac{2!}{1!(2-1)!} \times \frac{3!}{2!(3-2)!} \]
\[ C(2, 1) \times C(3, 2) = 2 \times \frac{3!}{2! \cdot 1!} \]
\[ C(2, 1) \times C(3, 2) = 2 \times \frac{3 \cdot 2}{2} \]
\[ C(2, 1) \times C(3, 2) = 2 \times 3 \]
\[ C(2, 1) \times C(3, 2) = 6 \]
So, there are 6 ways to form a committee with 1 man and 2 women.
b) Determine the number of 5 card combinations out of a deck of 52 cards, if there is exactly one ace in each combination.
Answer–
In a standard deck of 52 cards, there are 4 aces. To form a 5-card combination in which exactly one ace is included:
Selecting one ace
– The number of ways to choose 1 ace from the 4 available aces is \(4C1 = \frac{4!}{1!(4-1)!} = 4\).
Selecting the remaining 4 cards from the non-ace cards
– The number of ways to choose 4 cards from the remaining 48 non-ace cards is \(48C4 = \frac{48!}{4!(48-4)!} = 194,580\).
Using the multiplication principle, the total number of 5-card combinations with exactly one ace is given by:
\[ 4C1 \times 48C4 = 4 \times 194,580 = 778,320 \]
Therefore, there are 778,320 different 5-card combinations in a deck of 52 cards where exactly one ace is included.
5.Answer any one out of the following questions.
Prove the following by using the principle of mathematical induction for all n ∈ N:
a)1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
Answer–
To prove the given statement using mathematical induction, we’ll follow the steps of mathematical induction.
Step 1: Base Case
Verify the statement for the base case, \(n = 1\):
\[1 \cdot 2 + 2 \cdot 2^2 = 2 = (1 – 1) \cdot 2^{1+1} + 2\]
The base case is true.
Step 2: Inductive Step
Assume the statement is true for \(k = m\), where \(m\) is a positive integer:
\[1 \cdot 2 + 2 \cdot 2^2 + 3 \cdot 2^3 + \ldots + m \cdot 2^m = (m – 1) \cdot 2^{m+1} + 2\]
Now, prove the statement for \(k = m + 1\):
\[1 \cdot 2 + 2 \cdot 2^2 + 3 \cdot 2^3 + \ldots + m \cdot 2^m + (m + 1) \cdot 2^{m+1}\]
By the induction hypothesis, we know that:
\[1 \cdot 2 + 2 \cdot 2^2 + 3 \cdot 2^3 + \ldots + m \cdot 2^m = (m – 1) \cdot 2^{m+1} + 2\]
Add \((m + 1) \cdot 2^{m+1}\) to both sides:
\[(m – 1) \cdot 2^{m+1} + 2 + (m + 1) \cdot 2^{m+1} = (m – 1) \cdot 2^{m+1} + (m + 1) \cdot 2^{m+1} + 2\]
Combine like terms:
\[m \cdot 2^{m+1} + 2 = (m + 1) \cdot 2^{m+1} + 2\]
The statement holds for \(k = m + 1\).
Conclusion:
By mathematical induction, the given statement is proven for all \(n \in \mathbb{N}\):
\[1 \cdot 2 + 2 \cdot 2^2 + 3 \cdot 2^3 + \ldots + n \cdot 2^n = (n – 1) \cdot 2^{n+1} + 2\]
b) Prove n (n + 1) (n + 5) is a multiple of 3
Answer–
To prove that \(n (n + 1) (n + 5)\) is a multiple of 3 for all \(n \in \mathbb{N}\), we can use the principle of mathematical induction.
Step 1: Base Case
Let’s check the statement for the base case, \(n = 1\):
\[1 \cdot (1 + 1) \cdot (1 + 5) = 2 \cdot 6 = 12\]
12 is a multiple of 3. The base case is true.
Step 2: Inductive Step
Assume the statement is true for \(k = m\), where \(m\) is a positive integer:
\[m \cdot (m + 1) \cdot (m + 5)\]
Now, prove the statement for \(k = m + 1\):
\[(m + 1) \cdot ((m + 1) + 1) \cdot ((m + 1) + 5) = (m + 1) \cdot (m + 2) \cdot (m + 6)\]
Expand and factor:
\[(m + 1) \cdot (m + 2) \cdot (m + 6) = m \cdot (m + 1) \cdot (m + 5) + 2 \cdot (m + 1) \cdot (m + 5)\]
By the induction hypothesis, \(m \cdot (m + 1) \cdot (m + 5)\) is a multiple of 3. Additionally, \(2 \cdot (m + 1) \cdot (m + 5)\) is also a multiple of 3 because it involves a product of three consecutive integers (one of which is divisible by 3).
Thus, \((m + 1) \cdot (m + 2) \cdot (m + 6)\) is a multiple of 3.
Conclusion:
By mathematical induction, we have shown that \(n (n + 1) (n + 5)\) is a multiple of 3 for all \(n \in \mathbb{N}\).
.
OR
a) Expand (x/3 + 2/y)4
Answer–
To expand \((\frac{x}{3} + \frac{2}{y})^4\), we can use the binomial theorem. The general form of the binomial theorem is:
\[ (a + b)^n = \sum_{k=0}^{n} C(n, k) \cdot a^{n-k} \cdot b^k \]
Here, \(C(n, k)\) represents the binomial coefficient, or “n choose k.”
For the given expression \((\frac{x}{3} + \frac{2}{y})^4\):
\[ n = 4, \, a = \frac{x}{3}, \, b = \frac{2}{y} \]
The expansion is given by:
\[ (\frac{x}{3} + \frac{2}{y})^4 = \sum_{k=0}^{4} C(4, k) \cdot (\frac{x}{3})^{4-k} \cdot (\frac{2}{y})^k \]
Now, let’s calculate the binomial coefficients and write out the expansion:
\[ C(4, 0) \cdot (\frac{x}{3})^4 \cdot (\frac{2}{y})^0 + C(4, 1) \cdot (\frac{x}{3})^3 \cdot (\frac{2}{y})^1 + C(4, 2) \cdot (\frac{x}{3})^2 \cdot (\frac{2}{y})^2 + C(4, 3) \cdot (\frac{x}{3})^1 \cdot (\frac{2}{y})^3 + C(4, 4) \cdot (\frac{x}{3})^0 \cdot (\frac{2}{y})^4 \]
Now, substitute the values for the binomial coefficients:
\[ 1 \cdot (\frac{x}{3})^4 \cdot 1 + 4 \cdot (\frac{x}{3})^3 \cdot (\frac{2}{y})^1 + 6 \cdot (\frac{x}{3})^2 \cdot (\frac{2}{y})^2 + 4 \cdot (\frac{x}{3})^1 \cdot (\frac{2}{y})^3 + 1 \cdot (\frac{x}{3})^0 \cdot (\frac{2}{y})^4 \]
Now, simplify the terms:
\[ \frac{x^4}{81} + \frac{8x^3}{27y} + \frac{24x^2}{9y^2} + \frac{32x}{3y^3} + \frac{16}{y^4} \]
Therefore, the expansion of \((\frac{x}{3} + \frac{2}{y})^4\) is:
\[ \frac{x^4}{81} + \frac{8x^3}{27y} + \frac{24x^2}{9y^2} + \frac{32x}{3y^3} + \frac{16}{y^4} \]
b) Find the remainder when 7103 is divided by 25
Answer–
To find the remainder when \(7^{103}\) is divided by 25, we can use the following approach:
\[7^{103} = 7^{50} \cdot 7^{50} \cdot 7^3\]
Now, let’s examine the powers of 7 modulo 25:
\[7^1 \equiv 7 \pmod{25}\]
\[7^2 \equiv 24 \pmod{25}\]
\[7^3 \equiv 23 \pmod{25}\]
\[7^4 \equiv 4 \pmod{25}\]
\[7^5 \equiv 28 \equiv 3 \pmod{25}\]
We can observe a pattern: \(7^1 \equiv 7\), \(7^2 \equiv -1\), \(7^3 \equiv -2\), \(7^4 \equiv 4\), \(7^5 \equiv 3\), and the pattern repeats every 4 powers.
Now, let’s express \(7^{103}\) in terms of this pattern:
\[7^{103} = (7^4)^{25} \cdot 7^3 \equiv 4^{25} \cdot 7^3 \equiv (-1)^{25} \cdot 7^3 \pmod{25}\]
\[7^{103} \equiv -7^3 \pmod{25}\]
\[7^{103} \equiv -343 \pmod{25}\]
\[7^{103} \equiv -18 \pmod{25}\]
Therefore, the remainder when \(7^{103}\) is divided by 25 is 18.
c) Find the last two digits of the number (13)10
Answer–
To find the last two digits of the number \( (13)^{10} \), we can use the binomial expansion:
\[ (13)^{10} = (170 – 1)^5 \]
Applying the binomial theorem:
\[ (170 – 1)^5 = 5C0 \cdot (170)^5 – 5C1 \cdot (170)^4 + 5C2 \cdot (170)^3 – 5C3 \cdot (170)^2 + 5C4 \cdot (170) – 5C5 \]
Simplifying further:
\[ = 5C0 \cdot (170)^5 – 5C1 \cdot (170)^4 + 5C2 \cdot (170)^3 – 5C3 \cdot (170)^2 + 5 \cdot (170) – 1 \]
This expression can be expressed as a multiple of 100 plus \( 5 \cdot (170) – 1 \):
\[ = 100K + 849 \]
Therefore, the last two digits are 49.
6.Answer any one out of the following questions.
a) A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced. The table shows the results of 1000 cases.
If a tyre is bought from this company, what is the probability that :
(i) it has to be substituted before 4000 km is covered?
Answer
To find the probability that a tire needs to be replaced before 4000 km is covered, we can use the data provided in the table. Let’s denote the event “tire replacement before 4000 km” as \( A \). The probability of \( A \), denoted as \( P(A) \), is given by the ratio of the number of cases where the tire is replaced before 4000 km to the total number of cases.
Given in the table:
– Number of cases where distance covered is less than 4000 km = 200
– Total number of cases = 1000
The probability \( P(A) \) is calculated as follows:
\[ P(A) = \frac{\text{Number of cases where distance covered is less than 4000 km}}{\text{Total number of cases}} \]
\[ P(A) = \frac{200}{1000} \]
\[ P(A) = \frac{1}{5} \]
Therefore, the probability that a tire needs to be replaced before 4000 km is covered is \( \frac{1}{5} \).
(ii) it will last more than 9000 km?
Answer–
To find the probability that a tire lasts more than 9000 km, let’s denote the event “tire lasts more than 9000 km” as \( B \). The probability of \( B \), denoted as \( P(B) \), is given by the ratio of the number of cases where the tire lasts more than 9000 km to the total number of cases.
Given in the table:
– Number of cases where distance covered is more than 9000 km = 150
– Total number of cases = 1000
The probability \( P(B) \) is calculated as follows:
\[ P(B) = \frac{\text{Number of cases where distance covered is more than 9000 km}}{\text{Total number of cases}} \]
\[ P(B) = \frac{150}{1000} \]
\[ P(B) = \frac{3}{20} \]
Therefore, the probability that a tire lasts more than 9000 km is \( \frac{3}{20} \).
(iii) it will need to be replaced after it has covered somewhere between 4000 km and 14000 km?
Answer-
To find the probability that a tire needs to be replaced after it has covered somewhere between 4000 km and 14000 km, let’s denote this event as \( C \). The probability of \( C \), denoted as \( P(C) \), is given by the ratio of the number of cases where the tire is replaced between 4000 km and 14000 km to the total number of cases.
Given in the table:
– Number of cases where distance covered is between 4000 km and 14000 km = 600
– Total number of cases = 1000
The probability \( P(C) \) is calculated as follows:
\[ P(C) = \frac{\text{Number of cases where distance covered is between 4000 km and 14000 km}}{\text{Total number of cases}} \]
\[ P(C) = \frac{600}{1000} \]
\[ P(C) = \frac{3}{5} \]
Therefore, the probability that a tire needs to be replaced after it has covered somewhere between 4000 km and 14000 km is \( \frac{3}{5} \).
b) Two players, Sangeet and Rashmi, play a tennis match. The probability of Sangeet winning the match is 0.62. What is the probability that Rashmi will win the match?
Answer-
Since there are only two possible outcomes in a tennis match (Sangeet wins or Rashmi wins), the probability of Rashmi winning the match is the complement of the probability of Sangeet winning.
Let \( P(S) \) be the probability of Sangeet winning and \( P(R) \) be the probability of Rashmi winning. The relationship between these probabilities is given by:
\[ P(R) = 1 – P(S) \]
Given that \( P(S) = 0.62 \), we can substitute this into the formula:
\[ P(R) = 1 – 0.62 \]
\[ P(R) = 0.38 \]
Therefore, the probability that Rashmi will win the match is \( 0.38 \).
c) A coin is tossed three times, consider the following events. P: ‘No head appears’, Q: ‘Exactly one head appears’ and R: ‘At Least two heads appear’. Check whether they form a set of mutually exclusive and exhaustive events.
Answer-
Given: A coin is tossed three times.
Events:
\[ A: \text{ ‘No head appears’} \]
\[ B: \text{ ‘Exactly one head appears’} \]
\[ C: \text{ ‘At least two heads appear’} \]
Sample space:
\[ S = \{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT\} \]
\[ A = \{TTT\} \]
\[ B = \{HTT, THT, TTH\} \]
\[ C = \{HHT, HTH, THH, HHH\} \]
We need to find \( A \cup B \cup C \) to check for exhaustive events:
\[ A \cup B \cup C = \{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT\} = S \]
Hence, \( A, B, \) and \( C \) are exhaustive events.
We need to find \( A \cap B, B \cap C, \) and \( A \cap C \) for checking mutually exclusive events:
\[ A \cap B = \emptyset \]
So, \( A \) and \( B \) are mutually exclusive.
\[ B \cap C = \emptyset \]
So, \( B \) and \( C \) are mutually exclusive.
\[ A \cap C = \emptyset \]
So, \( A \) and \( C \) are mutually exclusive.
Hence, \( A, B, \) and \( C \) form a set of mutually exclusive and exhaustive events.
OR
a) Find the range and coefficient of range of the following data.
(i) 63, 89, 98, 125, 79, 108, 117, 68
Answer-
Arrange the data in ascending order:
\[ 63, 68, 79, 89, 98, 108, 117, 125 \]
Find the range, which is the difference between the maximum and minimum values:
\[ \text{Range} = \text{Maximum value} – \text{Minimum value} \]
\[ \text{Range} = 125 – 63 = 62 \]
So, the range of the data set is 62.
Find the coefficient of range. The coefficient of range is calculated as:
\[ \text{Coefficient of Range} = \frac{\text{Range}}{\text{Mean}} \]
Find the mean (average) of the data set:
\[ \text{Mean} = \frac{63 + 68 + 79 + 89 + 98 + 108 + 117 + 125}{8} \]
\[ \text{Mean} = \frac{847}{8} = 105.875 \]
Calculate the coefficient of range:
\[ \text{Coefficient of Range} = \frac{62}{105.875} \]
So, the coefficient of range is approximately \(0.585\).
(ii) 43.5, 13.6, 18.9, 38.4, 61.4, 29.8
Answer-
Arrange the data in ascending order:
\[ 13.6, 18.9, 29.8, 38.4, 43.5, 61.4 \]
Find the range, which is the difference between the maximum and minimum values:
\[ \text{Range} = \text{Maximum value} – \text{Minimum value} \]
\[ \text{Range} = 61.4 – 13.6 = 47.8 \]
So, the range of the data set is 47.8.
Find the coefficient of range. The coefficient of range is calculated as:
\[ \text{Coefficient of Range} = \frac{\text{Range}}{\text{Mean}} \]
Find the mean (average) of the data set:
\[ \text{Mean} = \frac{13.6 + 18.9 + 29.8 + 38.4 + 43.5 + 61.4}{6} \]
\[ \text{Mean} = \frac{206.6}{6} \approx 34.43 \]
Calculate the coefficient of range:
\[ \text{Coefficient of Range} = \frac{47.8}{34.43} \]
So, the coefficient of range is approximately \(1.39\).
b) If the range and the smallest value of a set of data are 36.8 and 13.4 respectively, then find the largest value.
Answer-
The range of a data set is the difference between the largest and smallest values. If the range is given as 36.8 and the smallest value is 13.4, we can use the formula for the range:
\[ \text{Range} = \text{Largest value} – \text{Smallest value} \]
Given that the range is 36.8 and the smallest value is 13.4, we can substitute these values into the formula:
\[ 36.8 = \text{Largest value} – 13.4 \]
Now, solve for the largest value:
\[ \text{Largest value} = 36.8 + 13.4 \]
\[ \text{Largest value} = 50.2 \]
Therefore, the largest value is 50.2.
c) A teacher asked the students to complete 60 pages of a record note book. Eight students have completed only 32, 35, 37, 30, 33, 36, 35 and 37 pages. Find the standard deviation of the pages yet to be completed by them.
Answer-
To find the standard deviation of the pages yet to be completed by the students, follow these steps:
Calculate the mean (average) of the pages completed.
\[ \text{Mean} = \frac{\sum x}{n} \]
where \( \sum x \) is the sum of the data values and \( n \) is the number of data values.
\[ \text{Mean} = \frac{32 + 35 + 37 + 30 + 33 + 36 + 35 + 37}{8} \]
\[ \text{Mean} = \frac{275}{8} = 34.375 \]
Create a table of the deviations from the mean for each student.
\[
\begin{array}{|c|c|c|}
\hline
\text{Student} & \text{Pages Completed} & \text{Deviation (\(X – \text{Mean}\))} \\
\hline
1 & 32 & -2.375 \\
2 & 35 & 0.625 \\
3 & 37 & 2.625 \\
4 & 30 & -4.375 \\
5 & 33 & -1.375 \\
6 & 36 & 1.625 \\
7 & 35 & 0.625 \\
8 & 37 & 2.625 \\
\hline
\end{array}
\]
Square each deviation.
\[
\begin{array}{|c|c|c|}
\hline
\text{Student} & \text{Pages Completed} & \text{Deviation (\(X – \text{Mean}\))} & \text{Deviation Squared} \\
\hline
1 & 32 & -2.375 & 5.640625 \\
2 & 35 & 0.625 & 0.390625 \\
3 & 37 & 2.625 & 6.890625 \\
4 & 30 & -4.375 & 19.140625 \\
5 & 33 & -1.375 & 1.890625 \\
6 & 36 & 1.625 & 2.640625 \\
7 & 35 & 0.625 & 0.390625 \\
8 & 37 & 2.625 & 6.890625 \\
\hline
\end{array}
\]
Find the sum of the squared deviations.
\[ \sum (X – \text{Mean})^2 = 43.10546875 \]
Step 5: Divide the sum of squared deviations by the number of data values.
\[ \text{Variance} = \frac{\sum (X – \text{Mean})^2}{n} \]
\[ \text{Variance} = \frac{43.10546875}{8} \]
\[ \text{Variance} = 5.38818359375 \]
Take the square root of the variance to find the standard deviation.
\[ \text{Standard Deviation} = \sqrt{\text{Variance}} \]
\[ \text{Standard Deviation} \approx \sqrt{5.38818359375} \approx 2.32 \]
Therefore, the standard deviation of the pages yet to be completed by the students is approximately \(2.32\).
