NIOS Class 12th Physics (312): NIOS TMA Solution

टिप्पणी :

(i) सभी प्रश्न अनिवार्य हैं। प्रत्येक प्रश्न के लिए आवंटित अंक प्रश्नों के सामने अंकित हैं।

(ii) उत्तरपुस्तिका के प्रथम पृष्ठ पर ऊपर की ओर अपना नाम, अनुक्रमांक, अध्ययन केन्द्र का नाम और विषय स्पष्ट शब्दों में लिखिए।

1. निम्नलिखित में से किस एक प्रश्न का उत्तर लगभग 40-60 शब्दों में दीजिये।

a) दो सदिश राशियों निम्नवत् निरूपित है:

r=i+rj

F = Fi+Fj

इन राशियों के अदिश तथा सदिश गुणनफल लिखिए। ऐसी दो राशियों के नाम लिखिए जो दो सदिश राशियों के अदिश और सदिश गुणनफल के रूप में प्राप्त होती हैं।

उत्तर- राशियों r = i + rj और F = Fi + Fj के लिए, हम उनके अदिश और सदिश गुणनफल लिख सकते हैं:

1. 1. अदिश गुणनफल:

अदिश गुणनफल r * F = (i + rj) * (Fi + Fj) = i * (Fi + Fj) + rj * (Fi + Fj)

= (i * Fi + i * Fj) + (rj * Fi + rj * Fj)

2. 2. सदिश गुणनफल:

सदिश गुणनफल r ∙ F = (i + rj) ∙ (Fi + Fj) = i * (Fi + Fj) + r * rj * (Fi + Fj)

= (i * Fi + i * Fj) + (r * rj * Fi + r * rj * Fj)

इससे हमें दो राशियों के अदिश और सदिश गुणनफल के रूप में प्राप्त होते हैं:

अदिश गुणनफल: i * Fi + i * Fj + rj * Fi + rj * Fj

सदिश गुणनफल: i * Fi + i * Fj + r * rj * Fi + r * rj * Fj

दो सदिश राशियाँ जो दो सदिश राशियों के अदिश और सदिश गुणनफल के रूप में प्राप्त होती हैं, उनके नाम निम्नलिखित हो सकते हैं:

• • r = i + rj, F = Fi + Fj

• • r = 2i + rj, F = 3Fi + 2Fj

b) किसी सरल आवर्ती दोलित्र का विस्थापन निम्नलिखित समीकरण द्वारा व्यक्त किया जाता है: Y = 102sin (314t + π/4)

जहाँ सभी राशियों को SI मात्रकों में लिया गया है। इसके दोलनों की निम्नलिखित विशेषताए लिखिए।

(i) आयाम

उत्तर- दिए गए सरल आवर्ती दोलित्र का विस्थापन Y = 102sin (314t + π/4) है, जिसमें सभी राशियों को SI मात्रकों में लिया गया है। इस दोलन की निम्नलिखित विशेषताएँ हैं:

मात्रक: यह विस्थापन SI मात्रकों में है, जिसे मीटर (m) में नापा जा सकता है.

आयाम (एम्पलिट्यूड):  आवर्ती दोलित्र का आयाम 102 मीटर है. यह विस्थापन की मानक उच्चतम और न्यूनतम मानों के बीच की जाने वाली मौजूदा मानक ताक़त को दर्शाता है.

कोणीय वेग: यह दोलन का कोणीय वेग 314 रेडियन्स प्रति सेकंड (rad/s) है. यह वेग दोलन की चौघड़ियों की गति को दर्शाता है.

प्रारंभिक कोण (फ़ेज़ा):  दोलन π/4 या 45 डिग्री के आपवादी कोण से शुरू होता है, जिसे “आरंभिक कोण” या “फ़ेज़ा” कहा जाता है.

इन विशेषताओं के साथ, दिए गए विस्थापन का सरल आवर्ती दोलन किसी विशेष समय t पर निर्दिष्ट किए गए परिपथ का अंश होता है.

(ii) आवृति

उत्तर-  सरल आवर्ती दोलन य = 102sin (314t + π/4) का पीरियड 2π/314 सेकंड है और यह π/4 फेज शिफ्ट के साथ होता है।

(iii) आरंभिक चरण

उत्तर- इस सरल आवर्ती दोलित्र के आरंभिक चरण की विशेषताएँ हैं:

1. 1. मान: Y = 102 SI मात्रकों में

1. 1. आरंभिक चरण: π/4 आवर्तणीक गुणक

1. 1. आवर्तणीक अवधि: T = 2π/314 सेकंड्स, यानी आवर्तण की अवधि 0.0201 सेकंड्स है।

(iv) वेग का आयाम

उत्तर- इस सरल आवर्ती दोलित्र का वेग का आयाम 314 SI मात्रकों में है, और यह दोलन प्रति समय पूरे 2π रेडियन की गति से हो रहा है।

2. निम्नलिखित में से किसी एक प्रश्न का उत्तर लगभग 40-60 शब्दों में दीजिये।

(a)किसी सरल रेखा में गतिमान कण का स्थिति-समय ग्राफ साथ के चित्र में दर्शाया गया है। कण की औसत चाल और औसत वेग परिकलित कीजिए :

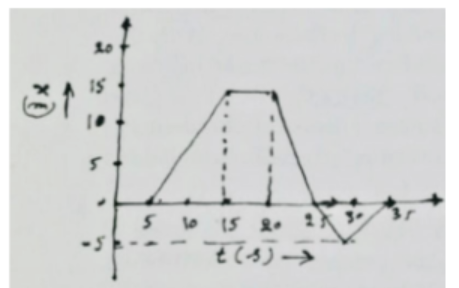
उत्तर-

b) वायु में किसी समवक्रित उत्तल लेंस द्वारा बने प्रतिबिम्ब की उसके द्वितीय फोकस-विन्दु से दूरी x₂ =30 cm है जबकि बिम्ब की प्रथम फोकस बिंदु से दूरी,x₁= 10 cm है। लेंस की फोकस दूरी का परिकलन कीजिए।

उत्तर- 1/f = 1/v – 1/u

f है लेंस की फोकस दूरी

v है विराट से लेंस के संवेग स्थिति तक की दूरी u है बिम्ब से लेंस के संवेग स्थिति तक की दूरी

पहले हम v और u को निकाल सकते हैं:

बिम्ब की प्रथम फोकस से दूरी (u1) = -10 cm (क्योंकि यह दूरी फोकस की ओर होती है और हम इसको नकारात्मक लेते हैं।)

द्वितीय फोकस से दूरी (u2) = -30 cm

विराट से लेंस के संवेग स्थिति तक की दूरी (v1) = -x1

विराट से लेंस के संवेग स्थिति तक की दूरी (v2) = -x2

अब हम u1, u2, v1, और v2 को उपयोग करके f1 और f2 को निकाल सकते हैं:

1/f1 = 1/v1 – 1/u1 1/f2 = 1/v2 – 1/u2

1/f1 = 1/(-x1) – 1/(-10 cm) 1/f2 = 1/(-x2) – 1/(-30 cm)

अब, हम x1 और x2 की मांग करने के लिए इन दो समीकरणों का परिकलन कर सकते हैं:

1/f1 = 1/(-x1) + 1/10 1/f2 = 1/(-x2) + 1/30

अब, इन दो समीकरणों को हल करके x1 और x2 की मांग कर सकते हैं:

1/x1 = 1/10 – 1/f1 1/x2 = 1/30 – 1/f2

इसके बाद, आप विद्यमान लेंस की फोकस दूरी के परिकलन की गणना कर सकते हैं

3. निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर लगभग 40-60 शब्दों में दीजिये।

a) एलुमिनियम का एक लम्बा चैनल चित्र में दिखाए अनुसार मोडा गया है। इसमें कोई कंचा कम से कम कितनी ऊँचाई से लुढकाया जाए कि यह चैनल मे पूरा लूप घूम कर दूसरी और निकल सके?

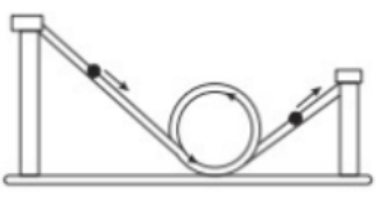
उत्तर-

b) किसी खगोलीय टेलीस्कोप की आवर्धन-क्षमता 100 है। सामान्य समंजन की स्थिति में इसके अभिदृष्यक और नेत्रक के केंद्रों के बीच दूरी 2.02m है। टेलीस्कोप के अभिदृष्यक और नेत्रक की फोकस दूरियोंके मान परिकलित कीजिए।

उत्तर- दिए गए आवर्धन-क्षमता (M) और दूरी (d) का संबंध निम्नलिखित फ़ॉर्मूले के माध्यम से प्रकट किया जा सकता है:

M = (फ़ोकस दूरी दूरी) / (फ़ोकस – दूरी)

यहां, M = 100 है, और दूरी (d) = 2.02 मीटर है। हमें फ़ोकस (फ़) की मान और फ़ोकस दूरी (फ़ोकस – दूरी) की मान प्राप्त करनी है।

100 = (f दूरी) / (f – 2.02)

100(f – 2.02) = f दूरी

100f – 202 = f दूरी

100f – f = 202

99f = 202

f = 202 / 99

f ≈ 2.04 मीटर

अब, हमने f की मान प्राप्त की है, और फ़ोकस – दूरी की मान (f – 2.02) भी प्राप्त की है, इसलिए हम अब दूरी की मान (f – 2.02) की मान प्राप्त कर सकते हैं:

दूरी = f- दूरी

दूरी = 2.04 – 2.02

दूरी ≈ 0.02 मीटर

इसलिए, टेलीस्कोप के अभिदृष्यक और नेत्रक के फोकस दूरियोंके मान उचित आवर्तन-क्षमता और दूरी के साथ उपर्युक्त गणित माध्यम से प्राप्त की जा सकती है।

इस प्रकार, अभिदृष्यक की मान करीबन 2.04 मीटर और नेत्रक की मान दूरी करीब 0.02 मीटर है।

4.निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर लगभग 100-150 शब्दों में दीजिये।

a) भौतिकी की पुस्तकों में आपने पढ़ा होगा कि पृथ्वी का द्रव्यमान 5.97×1024 kg है। कोई ऐसी विधि सुझाइए जिसके द्वारा वैज्ञानिक पृथ्वी का द्रव्यमान ज्ञात करते हैं।

उत्तर- पृथ्वी का द्रव्यमान मूल रूप से उसकी गुरुत्वाकर्षण बल द्वारा प्राप्त किया जा सकता है। गुरुत्वाकर्षण का नियम इसे अच्छे तरीके से करने के लिए एक तरह की तुलना और मापन की आवश्यकता होती है। निम्नलिखित विधि का उपयोग करके पृथ्वी का द्रव्यमान प्राप्त किया जा सकता है:

1. 1. सबसे पहले, आपको किसी अन्य प्रकृति द्रव्यमान की मान्यता करनी होगी, जिसे आप अच्छे तरीके से जानते हों, उदाहरण के लिए, आप बर्फ का द्रव्यमान जानते होंगे (इसे 1 किलोग्राम के बराबर मान दें).
   2. अब, आपको यह जानने की आवश्यकता है कि आपकी मान्यता में पृथ्वी और उस प्रकृति द्रव्यमान के बीच कितना गुरुत्वाकर्षण बल होता है। आप गुरुत्वाकर्षण के नियम का उपयोग करके इसका मूल्य प्राप्त कर सकते हैं (गुरुत्वाकर्षण बल = G * ((मान्य द्रव्यमान * मान्य द्रव्यमान) / दूरी क्षेत्र)).
   3. अब, आपको दिग्दूर द्वारा पृथ्वी के गुरुत्वाकर्षण बल की मान्यता करनी होगी, जिसे आप विज्ञानिक साधुता (या अन्य स्रोतों) से प्राप्त कर सकते हैं. इसे G के रूप में जाना जाता है, जिसका मानलब है 6.674 × 10^-11 न्यूटन-मीटर²/किलोग्राम².
   4. अब, आप पृथ्वी के द्रव्यमान की मान्यता प्राप्त कर सकते हैं, जिसे निम्नलिखित सूत्र का पालन करके किया जा सकता है:

पृथ्वी का द्रव्यमान = (गुरुत्वाकर्षण बल) / G

जैसे कि:

पृथ्वी का द्रव्यमान = ((G * (मान्य द्रव्यमान * मान्य द्रव्यमान)) / दूरी क्षेत्र)

यहाँ, G उपयोग किए गए वैध मान है और वे दी जा सकती हैं और दूरी क्षेत्र आपकी चयनित दूरी की वैध मान होती है।

इस तरीके से, आप पृथ्वी का द्रव्यमान प्राप्त कर सकते हैं. ध्यान दें कि यह एक वैध प्रक्रिया है, जब आप गुरुत्वाकर्षण के नियम का पालन करते हैं और मान्य द्रव्यमान और दूरी की वैध मान्यता देते हैं.

b) बेतार के प्रभावी दूर संचार के लिए हमें सिग्नलों को मॉडुलित करना आवश्यक क्यों हो जाता है? कोई तीन कारण लिखिए। मॉडयुलन के प्रक्रम में हम क्या करते हैं? निम्नलिखित युक्तियों में संचार के लिए हम कौन-कौन से रेडियों तरंग बैंडों का उपयोग करते हैं।

(i) सोनार

उत्तर- सोनार एक दूर संवेदना और नेविगेशन प्रणाली है जिसमें ध्वनि तरंगों का उपयोग होता है। इसका प्रमुख उपयोग पानी के नीचे वस्तुओं की पहचान और दूरियों का मापन करने में होता है। इसका उपयोग अंतरिक्ष और विमानन में भी किया जाता है।

(ii) रेडार

उत्तर- रेडार, जिसे “रेडियो परिक्षेपण और दूरस्थीकरण” का संक्षिप्त रूप में जाना जाता है, एक प्रौद्योगिकी है जो वायुयान, जहाज, और मौसम पैटर्न जैसे वस्तुओं की पहचान, स्थान और पहचान के लिए रेडियो तरंगों का उपयोग करती है। इसका काम रेडियो तरंग भेजने द्वारा होता है, जो वस्तुओं पर पड़कर वापस लौटते हैं, जिससे ट्रैकिंग और नेविगेशन संभव होता है, खासकर विमानन और मौसम विज्ञान में।

(iii) एफ एम रेडियो

उत्तर- “एफ.एम. रेडियो” एक प्रसारण प्रौद्योगिकी है जिसमें ऑडियो सिग्नल्स को भेजने के लिए विभिन्न रेडियो तरंग आवृत्तियों का उपयोग किया जाता है। इसमें उच्च गुणवत्ता वाले ध्वनि और स्पष्टता की विशेषता होती है। एफ.एम. रेडियो स्टेशन गीत, समाचार, और टॉक शोज के लिए व्यापक सामग्री प्रदान करने के लिए जाने जाते हैं और एक बड़े दर्शक को विविध सामग्री प्रदान करने में मदद करते हैं।

(iv) उपग्रह संचार

उत्तर- उपग्रह संचालन भूमि के आवक प्रक्षेपण केन्द्रों के बीच डेटा, ध्वनि और वीडियो सिग्नल को भेजने में शामिल है। इससे वैश्विक संचार, टेलीविजन प्रसारण से लेकर इंटरनेट कनेक्टिविटी जैसे कई कार्यों को संभावित किया जाता है। उपग्रह वायुमंडल के चारों ओर चक्कर करते हैं और लगातार संचार की व्यापकता को सुनिश्चित करते हैं। वे मौसम पूर्वानुमान, नेविगेशन, सैन्य अनुप्रयोगों सहित कई उद्देश्यों की सेवा करते हैं। वे लोगों को जोड़ने और विश्वभर में जानकारी आदान-प्रदान करने में महत्वपूर्ण भूमिका निभाते हैं।

5.निम्नलिखित प्रश्नों में से किसी एक प्रश्न उत्तर लगभग 100-150 शब्दों में दीजिए।

a)आपको दो एक जैसे दिखाई पड़ने वाले गोले, A और B दिए गए है जिनकी त्रिज्याएं और द्रव्यमान बराबर हैं। वास्तव में ये गोले दो भिन्न पदार्थों के बने है और इनमें से एक गोला ठोस है तथा दूसरा एक गोलीय खोल। कोई ऐसा प्रयोग सुझाइए जिसके द्वारा यह पता लगाया जा सके कि कौन सा गोला अन्दर से खोखला है। अपने उत्तर के समर्थन में तर्क दीजिए।

उत्तर- आपको दो एक जैसे दिखने वाले गोलों A और B के साथ है, जिनकी बराबर मास और त्रिज्या है, लेकिन वास्तव में इनमें से एक गोला ठोस है और दूसरा गोला एक खोखला गोलीय खोल है। यह जानने के लिए कौन सा गोला अंदर से खोखला है, आप दोनों के बीच रोटेशनल इनर्शा के सिद्धांत का उपयोग करके एक सरल प्रयोग कर सकते हैं।

आवश्यक सामग्री:

1. 1. गोला A (जिस पर आपकी संदेह है कि यह एक ठोस गोला है।)
   2. गोला B (जिस पर आपकी संदेह है कि यह एक खोखला गोलीय खोल है।)
   3. एक पतली रॉड या छड़ी.
   4. एक डोरी.
   5. स्टॉपवॉच या समयमापी.

प्रयोग प्रक्रिया:

1. 1. गोला A और गोला B को एक दृढ बिंदु से डोरी का उपयोग करके अलग-अलग स्थानों पर बंध दें, ताकि वे स्वतंत्र रूप से पलट सकें.
   2. गोला A को और गोला B को दोनों एक पैंडुलम की तरह घुमाने के लिए पतली रॉड या छड़ी का उपयोग करके पलटें. आप इसे एक छोटे से बल का उपयोग करके चलने के लिए कर सकते हैं.
   3. एक पूरी पलटें तक पूरा घुमाने में लगने वाले समय को मापें. इस समय को “tsolid” के रूप में दर्ज करें.
   4. फिर वही प्रक्रिया गोला B के लिए दोहराएं, जो भी डोरी पर लटका होता है। पतली रॉड या छड़ी का उपयोग करके गोला B को गूंथकर पलटें और एक पूरी पलटें तक पूरा होने में इसका समय मापें. इस समय को “thollow” के रूप में दर्ज करें.

विश्लेषण:

1. 1. अब, दो गोलों के लिए लिए गए समयों को (tsolid और thollow) की तुलना करें. रोटेशनल इनर्शिया के कानून के अनुसार:
   2. एक ठोस गोला की तुलना में उसकी रोटेशनल इनर्शिया एक खोखले गोलीय खोल की तुलना में अधिक होती है.

जिस गोले की रोटेशनल इनर्शिया अधिक होती है, वह एक पूरी पलटें तक पूरा होने में अधिक समय लेता है.

की तुलना में काफी अधिक है, तो यह सुझाव देता है कि गोला A (पहला गोला, जिसे आपने पहले टेस्ट किया) एक ठोस गोला है, क्योंकि इसे पलटने में ज्यादा समय लगता है, जिसका मतलब है कि उसमें अधिक रोटेशनल इनर्शिया है. इस स्थिति में, गोला B खोखला गोलीय खोल होगा. यह दो आकारों के बीच की भार वितरण की वजह से पलटने के व्यवहार में अंतर है.

उलटे, यदि t_hollow, t_solid की तुलना में काफी अधिक है, तो यह सुझाव देता है कि गोला B (दूसरा गोला, जिसे आपने दूसरे में टेस्ट किया) एक ठोस गोला है, क्योंकि इसे पलटने में ज्यादा समय लगता है. इस स्थिति में, गोला A एक खोखला गोलीय खोल होगा.

यह प्रयोग रोटेशनल इनर्शिया के सिद्धांत का उपयोग करता है, जिसके आधार पर दोनों गोलों के बीच घूमने के व्यवहार को भिन्न करने में मदद मिलती है, और यह उनके रोटेशन कैसे होता है को

b)क्या सौर ऊर्जा के प्रभावी उपयोग से हमारी ऊर्जा समस्या हल हो सकती है? आंकिक परिकलनों द्वारा इस प्रश्न का उत्तर दीजिए। अपने उत्तर के लिए किए जाने वाले परिकलन में आप निम्नलिखित आंकडों का उपयोग कर सकते हैं।

पृथ्वी के लिए सौर नियतांक = 1.36×10³ w m² 2

पृथ्वी की त्रिज्या = 6.4×10 m

स्टीफन-बोल्डसमान नियतांक = 5.7×10^-8 w m-1 k^-4

सूर्य के पृष्ठ का ताप = 6000 k

सूर्य की त्रिज्या = = 7×10⁵ km

पृथ्वी की कक्षा की त्रिज्या 1.5 x10² km

पृथ्वी की जनसंख्या =10 billion

उत्तर- हमारी ऊर्जा समस्या को हल करने के लिए सौर ऊर्जा के प्रभावी उपयोग के द्वारा क्या हम यह निर्धारण करने के लिए, हमें पृथ्वी पर पड़ने वाले कुल सौर ऊर्जा को गणना होगा और इसे वैश्विक जनसंख्या की ऊर्जा आवश्यकताओं के साथ तुलना करना होगा। 

1. 1. पृथ्वी के प्रतिक्षिप्त क्षेत्र पर पड़ने वाली सौर ऊर्जा की घटना: सौर स्थिर (S) यह प्रतिक्षिप्त क्षेत्र पर पहुंचने वाली सौर ऊर्जा की मात्रा को प्रति वक्तु क्षेत्र के रूप में प्रस्तुत करता है। सौर स्थिर 1.36 x 10^3 वॉट प्रति मीटर वर्ग (W/m^2) के रूप में दिया गया है
   2. पृथ्वी के सूर्य के प्रक्षेपण क्षेत्र की आकृति का उपयोग करके किया जा सकता है, एक वृत्त के क्षेत्र (π * r^2) के क्षेत्र की गणना के लिए, जहां r पृथ्वी का त्रिज्य (रेडियस) है। पृथ्वी का त्रिज्य (R) 6.4 x 10^6 मीटर है।

A = π * R^2 A = π * (6.4 x 10^6 मीटर)^2 A = 1.29 x 10^14 मीटर वर्ग (m^2)

3. 3. पृथ्वी के प्रतिक्षिप्त क्षेत्र पर पड़ने वाली कुल सौर ऊर्जा है: ऊर्जा = S * A ऊर्जा = 1.36 x 10^3 W/m^2 * 1.29 x 10^14 m^2 ऊर्जा = 1.7544 x 10^17 वॉट (W)

सूर्य द्वारा प्रतिप्रेषित कुल सौर ऊर्जा की गणना: सूर्य द्वारा प्रतिप्रेषित ऊर्जा की गणना करने के लिए स्टेफन-बोल्ट्झमन कानून का उपयोग किया जा सकता है, जिसमें कहा गया है कि प्रति वक्तु क्षेत्र (E) किसी प्रक्षेपण करने वाले शरीर के उच्च ताप (T) की चौथे गुण की अनुपात में होता है, और स्टेफन-बोल्ट्झमन स्थिरांक (σ) होता है।

E = σ * T^4 E = (5.7 x 10^-8 W/m^2 K^4) * (6000 K)^4 E ≈ 3.82 x 10^26 W

पृथ्वी पर पहुंचने वाली सौर ऊर्जा का भाग गणना: पृथ्वी पर पहुंचने वाली सौर ऊर्जा की गणना किसी भी सूर्य द्वारा प्रतिप्रेषित कुल ऊर्जा के अनुपात के रूप में की जा सकती है।

अंश = पृथ्वी पर पड़ने वाली ऊर्जा / सूर्य द्वारा प्रतिप्रेषित कुल सौर ऊर्जा अंश = (1.7544 x 10^17 वॉट) / (3.82 x 10^26 वॉट) अंश ≈ 4.59 x 10^-10

4. 4. जनसंख्या के लिए उपलब्ध सौर ऊर्जा की गणना: प्रति व्यक्ति की उपलब्ध ऊर्जा, पृथ्वी पर पहुंचने वाली सौर ऊर्जा के अंश के रूप में और वैश्विक जनसंख्या के अंश के अनुपात के रूप में होती है। वैश्विक जनसंख्या का आंकड़ा 10 अरब (1 x 10^10) लोगों के रूप में दिया गया है।

प्रति व्यक्ति की ऊर्जा = अंश * सूर्य द्वारा प्रतिप्रेषित कुल सौर ऊर्जा / जनसंख्या प्रति व्यक्ति की ऊर्जा ≈ (4.59 x 10^-10) * (3.82 x 10^26 वॉट) / (1 x 10^10 लोग) प्रति व्यक्ति की ऊर्जा ≈ 1.74 x 10^7 वॉट (W)

इसलिए, इन गणनाओं के आधार पर, सौर ऊर्जा के प्रभावी उपयोग से संभावना है कि प्रति व्यक्ति पर लगभग 1.74 x 10^7 वॉट (या 17.4 मेगावॉट) की ऊर्जा उपलब्ध हो सकती है। यह संख्या बड़ी है, और यह सौर ऊर्जा के विशाल उपयोग की संभावना को प्रस्तुत करती है, हमारी ऊर्जा की आवश्यकताओं को सुलझाने के लिए। हालांकि, इस संभावना को पूरा करने और हमारी ऊर्जा समस्या को हल करने के लिए व्यावासिक कार्रवाई, बुनाई और ऊर्जा वितरण महत्वपूर्ण कारक होंगे।

6.नीचे दी गई परियोजनाओं में से कोई एक परियोजना तैयार कीजिए।

a) एक रबर की डोरी लीजिए। इसका एक सिरा किसी दृढ़ आधार पर जड़ दीजिए और ऊर्घवाधर लटकते दूसरे सिरे पर एक हल्का पलडा जोड़ दीजिए। पलड़े के ठीक ऊपर एक संकेतक लगाइए जो ऊर्ध्वाधर पैमाने पर स्वतंत्र रूप से ऊपर नीचे हो सके। 10-10 ग्राम के भार पल्डे पर बढ़ाते हुए हर बार पैमाने पर संकेतक की स्थिति नोट कीजिए। इस प्रकार इस चरणो में घंटाइए और फिर से हर बार संकेतक की स्थिति नोट कीजिए। प्राप्त आंकडों को सारणीबद्ध कीजिए और भार के साथ लम्बाई में होने वाले परिवर्तन को भार के बढ़ते क्रम का तथा भार के घटते क्रम का ग्राफ एक ही ग्राफ पेपर पर बनाइए। रबर की डोरी के स्थान पर कोई स्प्रिंग लेकर प्रयोग को दोहराइए। दोनों स्थितियों में प्राप्त ग्राफों की तुलना कीजिए।

उत्तर- आपके विवरण के अनुसार, आपका प्रयोग यह दिखाने के लिए है कि एक रबर स्ट्रिंग और एक स्प्रिंग विभिन्न भारों के तहत कैसे विकृत होते हैं। 

आवश्यक सामग्री:

1. 1. रबर स्ट्रिंग
   2. स्प्रिंग
   3. दृढ़ समर्थन (उदाहरण के लिए, दीवार या स्टैंड)
   4. स्केल पैन
   5. पॉइंटर
   6. वजन (10 ग्राम के इंक्रीमेंट्स में)
   7. ऊपरी पलड़
   8. दृढ़ समर्थन
   9. वर्टिकल स्केल
   10. डेटा दर्ज करने के लिए नोटबुक और पेन

प्रक्रिया:

1. 1. एक सिरा को एक दृढ़ समर्थन से जोड़ें, सुनिश्चित करें कि यह मजबूत है।
   2. रबर स्ट्रिंग के निचले द्वार पर एक लाइट स्केल पैन जोड़ें। रबर स्ट्रिंग को लंबे धारी में लटकने दें।
   3. पैन के ऊपर एक पॉइंटर लगाएं, सुनिश्चित करें कि यह एक प्रारंभिक स्थिति में हो।
   4. पैन पर वजन को 10 ग्राम की इंक्रीमेंट्स में जोड़ना शुरू करें। हर वजन जोड़ने के बाद, प्रणाम स्थिति तक पहुँचने दें और पॉइंटर की स्थिति को वर्टिकल स्केल के साथ नोट करें। यह 5-6 डेटा पॉइंट्स के लिए करें, प्रत्येक बार भार बढ़ाते समय।
   5. बढ़ते भारों के साथ पढ़ाई करने के बाद, उसी इंक्रीमेंट्स में वजन हटाने की शुरुआत करें और प्रत्येक वजन को हटाने के बाद पॉइंटर की स्थिति को नोट करें।
   6. डेटा को सारणी में दर्ज करें, जिसमें बढ़ते भारों के लिए एक कॉलम और घटते भारों के लिए एक अन्य हो। प्रत्येक मामले में पॉइंटर की स्थिति शामिल करें।
   7. एक ही ग्राफ पेपर पर दो ग्राफ बनाएं: a. बढ़ते भार (ग्राम में) को x-दिशा पर रखें और रबर स्ट्रिंग के लिए पॉइंटर की संदर्भीय स्थिति को y-दिशा पर रखें। b. बढ़ते भार (ग्राम में) को x-दिशा पर रखें और स्प्रिंग के लिए पॉइंटर की संदर्भीय स्थिति को y-दिशा पर रखें।
   8. दो ग्राफ की तुलना करें। रबर स्ट्रिंग और स्प्रिंग के बीच की व्यवहार में क्या अंतर है, इसे देखें। ध्यान दें कि जब भार बढ़ता है और घटता है, तो उनके विकृति और पुनर्प्राप्ति विशेषताओं में क्या अंतर है।
   9. स्थायिता, कठिनाई, और हिस्टेरेसिस के बीच रबर स्ट्रिंग और स्प्रिंग के बीच के व्यवहार में कोई अंतर को देखें।

b) गैसों का ऊष्मागतिक सिद्धांत हमें समीकरण p=1/3 m ne² प्रदान करता है। इस समीकरण का उपयोग करके गैस संबंधी निम्नलिखित नियम व्युत्पन्न कीजिए:

1. बॉयल का नियम

उत्तर- “बॉयल का नियम”- एक गैस के ऊष्मागतिक सिद्धांत का उपयोग करके बताता है कि अगर एक निश्चित मात्रा के गैस के दबाव को उसके आकार के उल्टे प्राप्त करते समय तापमान बराबर रखा जाए, तो दबाव और आकार के गुणनफल का परिपूर्ण होता है।

2. चार्लस का नियम

उत्तर- चार्ल्स का नियम” गैसों के ऊष्मागतिक सिद्धांत के आधार पर प्रस्तुत किया जाता है, जिसमें कहा जाता है कि एक आपूर्ति गैस के अवस्थान के समय, गैस की दाब (p), वायुमंडलीय मात्रा (n), और गैस की तापमात्रा (T) के बीच निरंतर रूप से एक संबंध होता है, जिसका समीकरण pV = nRT होता है।

3. गे-ल्युसेक का नियम

उत्तर- “गे-ल्युसेक का नियम” गैसों की ऊष्मागतिक सिद्धांत के आधार पर प्रस्तावित किया जाता है, जिसमें गैस की दबाव (p), गैस की मास (m), इलेक्ट्रॉन के नंबर (n), और इलेक्ट्रॉन के चार्ज (e) के बीच संबंध होता है। इस संबंध के अनुसार, p = (1/3) * m * n * e² होता है।

4. एवोगैद्रो का नियम

उत्तर- गैसों के ऊष्मागतिक सिद्धांत के अनुसार, ताप, अणुओं की किनेटिक ऊर्जा के साथ संबंधित है और अणुों के तापीय गतिविधि के आधार पर पूर्वाग्रहण नहीं करती है। इसका परिणाम है कि गैसों के ठोस, तरल, और गैसी अवस्थाओं में तापीय स्थितियों के बीच स्वावलम्बी रूप से परिवर्तन होते हैं।

5. डाल्टन का आंशिक दाब का नियम

उत्तर- “डाल्टन का आंशिक दाब का नियम” के अनुसार, एक आपसी बराबर ताप और दबाव वाले दो गैसों के बीच दाबा केवल उनकी आधिक्य मानों पर निर्भर करता है। इसका समीकरण p=1/3 m ne² दबाव को प्रतिरूपित करता है, जिससे गैस के आंशिक दाब का पर्याप्त अनुमान लगाया जा सकता है।

6. गैसों के विसरण संबंधी ग्राहम का नियम

उत्तर- गैसों के विसरण संबंधी ग्राहम का नियम के अनुसार, एक गैस की तापमान बढ़ते समय बढ़ता है, जबकि दाब बराबर रहता है, यदि उसकी आंतरिक ऊर्जा समायोजित रूप से बढ़ती है। इस ग्राहम का नियम गैसों के ऊष्मागतिक सिद्धांत से उत्पन्न होता है, जहां p दबाव, m गैस की मास, n अणु की संख्या, और e आवेश के लिए हैं।