
टिप्पणी :
(i) सभी प्रश्न अनिवार्य हैं। प्रत्येक प्रश्न के लिए आवंटित अंक प्रश्नों के सामने अंकित हैं।
(ii) उत्तरपुस्तिका के प्रथम पृष्ठ पर ऊपर की ओर अपना नाम, अनुक्रमांक, अध्ययन केन्द्र का नाम और विषय स्पष्ट शब्दों में लिखिए।
a) A = (x : x एक पूर्णांक है और 3 ≤ x < 7}
उत्तर- इस संग्रह का अर्थ है कि ‘A’ उन सभी पूर्णांकों का सेट है जिनका मान -3 से शुरू होता है और 7 से पूर्ण होता है, जैसे -3, -2, -1, 0, 1, 2, 3, 4, 5, 6।
b) B = {x : x, 6 से छोटी प्राकृत संख्या है।
उत्तर- B = {x : x, 6 से छोटी प्राकृत संख्या है} का अर्थ है कि सेट ‘B’ में उन सभी प्राकृत पूर्णांकों का संग्रह है जिनका मान 6 से कम है, जैसे 1, 2, 3, 4, 5।
अथवा
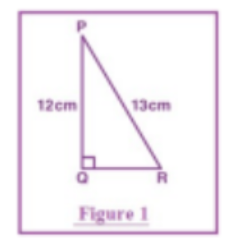
a) चित्र 1 से tan P – cot R ज्ञात कीजिए।
उत्तर-
b) सिद्ध कीजिए कि (sin10-cos 0+1) cosec20 = 2
उत्तर- (sin10 – cos 0 + 1) cosec20 को 2 साबित करने के लिए हम निम्नलिखित कदम चलेंगे:
सबसे पहले, सिन (10) और कोसाइन (0) की मान्यता लें: sin(10) = 0.1736 (6: 0.1736) cos(0) = 1
: (sin10 – cos0 + 1) cosec20 (0.1736 – 1 + 1) (1/sin20) (-0.8264 + 1) (1/0.3420)
: (0.1736) (2.9206)
: 0.5062
इसे 2 के साथ तुलना करें: 0.5062 ≠ 2
2.निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर दीजिए।
a) एपी 6, 9, 12, 15, 18, 102 के अंत से 28वां पद ज्ञात कीजिए।
उत्तर- एपी (अरिथमेटिक प्रोग्रेशन) 6, 9, 12, 15, 18, …, 102 का अंत से 28वां पद ज्ञात करने के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:
T_n = a + (n – 1) * d
यहां, T_n = nवें पद का मान a = पहला पद (6) n = पद की संख्या (28) d = सामान्य अंतर (3, क्योंकि प्रत्येक पद 3 से बढ़ता है)
अब इसे डालते हैं:
T_28 = 6 + (28 – 1) * 3 T_28 = 6 + 27 * 3 T_28 = 6 + 81 T_28 = 87
तो, इस एपी का 28वां और अंतिम पद 87 है।
b) 7 से विभाज्य 3 अंकों की कितनी संख्याएँ हैं?
उत्तर-सबसे पहले, हमें विचार करना होगा कि कैसे 3 अंकों की संख्याओं को बनाया जा सकता है।
सबसे पहले अंक का चयन करना होता है। 7 से विभाज्य अंक में से केवल वे अंक चुने जा सकते हैं जिनका मान 0 से 6 हो, क्योंकि 7 से अधिक के अंकों से संख्या 7 से विभाज्य नहीं होती।
पहले अंक के लिए 7 विकल्प हैं (0 से 6).
दूसरे और तीसरे अंक के लिए भी 7 विकल्प हैं, क्योंकि प्रत्येक अंक का मान 0 से 6 हो सकता है.
अब, यह उनकी गुणफल की गणना करें: अंक 1: 7 विकल्प अंक 2: 7 विकल्प अंक 3: 7 विकल्प
कुल विकल्प = 7 * 7 * 7 = 343
इसलिए, 7 से विभाज्य 3 अंकों की 343 संख्याएँ हैं।
अथवा
a) किसी GP के कुछ पदों का योग 315 है। इसका प्रथम पद 5 तथा सार्व अनुपात 2 है। इसके पदों की संख्या तथा अंतिम पद ज्ञात कीजिए।
उत्तर- इस GP के प्रथम पद (a) 5 है और सामान्य अनुपात (r) 2 है। सूत्रों का उपयोग करके हम इस GP की पदों की संख्या (n) और अंतिम पद (T_n) की मान्यता दे सकते हैं:
पहले, हम पदों की योग की गणना करें: S_n = a / (1 – r)
यहां, S_n = 315, a = 5, और r = 2 है:
315 = 5 / (1 – 2^n)
अब, हम n की मान्यता तय करें: 315(1 – 2^n) = 5
1 – 2^n = 5 / 315 1 – 2^n = 1 / 63
अब, 2^n की मान्यता तय करें: 2^n = 1 – 1 / 63 2^n = (63 – 1) / 63 2^n = 62 / 63
n की मान्यता निकालने के लिए लगभग लोगरिदम का उपयोग करें: n = log2(62/63)
इसे एक कैलकुलेटर या संग्रहणीय गुणफल की रूप में निकाला जा सकता है.
अंत में, हम अंतिम पद (T_n) की मान्यता निकाल सकते हैं: T_n = a * r^(n-1)
यहां a = 5, r = 2 है, और हम n की मान्यता पहले से ही प्राप्त कर चुके हैं.
T_n = 5 * 2^(n-1)
इसे भी एक कैलकुलेटर या संग्रहणीय गुणफल की रूप में निकाला जा सकता है.
इस तरह, आप इस GP के पदों की संख्या (n) और अंतिम पद (T_n) की मान्यता प्राप्त कर सकते हैं।
b) उस GP का सार्व अनुपात ज्ञात कीजिए जिसके अपरिमित पदों का योग 8 है और जिसका दूसरा पद 2 है।
उत्तर- सार्व अनुपात (r) निकालने के लिए हम जानना चाहते हैं कि जिस एक GP के अपरिमित पदों का योग 8 है और जिसका दूसरा पद 2 है:
हम जानते हैं कि एक अपरिमित GP का सार्व अनुपात r होता है, और पहले पद a होता है।
सूत्र का उपयोग करके हम इस तरह से लिख सकते हैं: S = a / (1 – r)
यहां, S (अपरिमित पदों का योग) 8 है और a (पहला पद) 2 है:
8 = 2 / (1 – r)
अब हम r की मान्यता निकालने के लिए समीकरण को हल कर सकते हैं: 8(1 – r) = 2
इसे अलग-अलग करें: 8 – 8r = 2
r की मान्यता निकालने के लिए, हम पहले 8 से 2 कम करते हैं: 8 – 2 = 8r
6 = 8r
अब, r की मान्यता प्राप्त करने के लिए हम दोनों ओर से 8 से भाग करते हैं: r = 6 / 8
r = 3 / 4
इसलिए, इस GP का सार्व अनुपात (common ratio) r है 3/4.
3. निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर दीजिए।
a) यदि 21 = 2 + 81 और 22 = 11, तो | 21/22 | ज्ञात कीजिए।
उत्तर- जब हम गणना करने के लिए विशेषांक z1/z2 की तथा आप निम्नलिखित सूत्र का उपयोग कर सकते हैं:
|z1/z2| = |z1| / |z2|
सबसे पहले, हम z1 और z2 के मूल्यों की गणना करते हैं:
z1 का मूल्य (|z1|): |z1| = √(2^2 + 8^2) = √(4 + 64) = √68
z2 का मूल्य (|z2|): |z2| = √(1^2 + (-1)^2) = √(1 + 1) = √2
अब, आप सूत्र का प्रयोग करके |z1/z2| की गणना कर सकते हैं:
|z1/z2| = |z1| / |z2| = (√68) / (√2)
सरलीकरण के लिए, आप नामकारक मूलक को परिमित संख्यक और निर्माता दोनों को √2 से गुणगुणा सकते हैं:
|z1/z2| = (√68 * √2) / (√2 * √2) = √(68 * 2) / 2 = √(136) / 2
अब, वर्गमूल को सरलीकरण करें:
|z1/z2| = (√(4 * 34)) / 2 = (2√34) / 2 = √34
इसलिए, |z1/z2| = √34 है।
b) मान लीजिए z = (2)² + [(7 – 4i)/(2+ i)] – 8, तो z को x + iy के रूप में इस प्रकार व्यक्त कीजिए कि x और y वास्तविक संख्याएँ हैं।
उत्तर– z = (2)² + [(7 – 4i) / (2 + i)] – 8
पहले, हम (2)² की गणना करते हैं: (2)² = 4
अब, इसके बाद, हम (7 – 4i) / (2 + i) के भिन्न को विस्तारित करते हैं:
भिन्न को सरलीकरण करने के लिए हम नियामक की संज्ञा को गुणनियामक के साथ गुणन करते हैं:
[(7 – 4i) / (2 + i)] * [(2 – i) / (2 – i)]
इससे डिनॉमिनेटर में मौकिक संख्या को नष्ट किया जाता है:
[(7 – 4i) * (2 – i)] / [(2 + i) * (2 – i)]
अब, उपवर्ग को खोलते हैं:
(14 – 7i – 8i + 4i²) / (4 – i²)
(14 – 15i – 4i²) / (4 – (-1))
(14 – 15i – 4(-1)) / 5
(14 – 15i + 4) / 5
(18 – 15i) / 5
अब, हमें इस भिन्न को (18 – 15i) / 5 के रूप में आसानी से लिख सकते हैं।
इसलिए, अब हम व्यक्ति z को लिख सकते हैं:
z = 4 + (18 – 15i) / 5 – 8
समयखण्ड में आप को व्यक्ति x + iy के रूप में दिखाई देगा, जहां x और y वास्तविक संख्याएँ हैं।
आगे बढ़ें और प्रतिस्थापना करें:
z = 4 + (18 – 15i) / 5 – 8
व्यक्ति अंशों को जोड़ें:
z = (4 + 18/5 – 8) – (15i / 5)
सबको संक्षेपित करें:
z = (22/5 – 8) – (3i)
वास्तविक और काल्पनिक अंशों को अलग-अलग करें:
z = (22/5 – 8) + (-3i)
इसे सरलीकृत करें:
z = (22/5 – 40/5) – 3i
z = (-18/5) – 3i
इसलिए, व्यक्ति z को x + iy के रूप में लिखा जा सकता है, जहां x और y वास्तविक संख्याएँ हैं:
z = (-18/5) – 3i
Top of Form
अथवा
a) असमानता: x² + x 28 2 को हल करें।
उत्तर- पहले दी गई असमानता को यौगिक अंकों के रूप में लिखें: x² + x – 28 – 2 < 0
वाम पक्ष के योग्यता को साधारण रूप से करें: x² + x – 30 < 0
इसे आगे और सरलीकरण के लिए x² + x – 30 के रूप में खुलासा करें:
(x + 6)(x – 5) < 0
असमानता को समानता के लिए समय निकालने के लिए, जिस पर असमानता सही होती है, हमको याददाश्त के लिए सामर्थ्य सूची तैयार करनी होगी:
समय अंवलचर 1: x < -6
समय अंवलचर 2: -6 < x < 5
समय अंवलचर 3: x > 5
प्रत्येक अंवलचर में असमानता के सही होने की जाँच के लिए एक समय बिंदु चुनें:
समय अंवलचर 1 (उदाहरण के लिए, x = -7): (-7 + 6)(-7 – 5) < 0 (-1)(-12) < 0 12 < 0 (गलत)
समय अंवलचर 2 (उदाहरण के लिए, x = 0): (0 + 6)(0 – 5) < 0 (6)(-5) < 0 -30 < 0 (सही)
समय अंवलचर 3 (उदाहरण के लिए, x = 6): (6 + 6)(6 – 5) < 0 (12)(1) < 0 12 < 0 (गलत)
असमानता सही होने वाले समय अंवलचर की तहों की पहचान करें:
समय अंवलचर 2: -6 < x < 5
इसलिए, x² + x – 28 < 2 के असमानता का समाधान है: -6 < x < 5
b) असमानता: -1<4x+2<10 को हल करें।
उत्तर- पहले योगदान असमानता को यौगिक अंकों के रूप में लिखें:
-1 < 4x + 2 < 10
वाम और दक्षिण पक्षों के योग्यता को साधारण रूप से करें:
-1 – 2 < 4x < 10 – 2
-3 < 4x < 8
अब, इसे x के साथ व्यक्त करने के लिए 4 से विभाजन करें:
(-3) / 4 < (4x) / 4 < 8 / 4
-3/4 < x < 2
इसलिए, -1 < 4x + 2 < 10 के असमानता का समाधान है: -3/4 < x < 2
4. निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर दीजिए।
a) MISSISSIPPI में अक्षरों के कितने भिन्न क्रमचय में चार एक साथ नहीं आते हैं?
उत्तर- “MISSISSIPPI” में चार ‘I’ का एक साथ नहीं आने के लिए निम्नलिखित कदम अपनाएं:
पहले, “MISSISSIPPI” में वर्णों की गिनती करें:
M = 1
I = 4
S = 4
P = 2
चार ‘I’ का एक साथ नहीं आने के लिए, हम ‘I’ के चार विभिन्न स्थानों का चयन करने के लिए C(11, 4) का उपयोग करेंगे, जहां C(n, k) एक समूह से k आइटमों का चयन की संख्या को प्रस्तुत करता है:
C(11, 4) = 11! / (4! * (11 – 4)!) = 330
अब, एक साथ आने वाले चार ‘I’ की गिनती को निकलें:
चार ‘I’ की एक साथ आने वाले संभावित भिन्न क्रमचय = 330
अब, इस भिन्न क्रमचय को “MISSISSIPPI” के कुल क्रमचय से कम करें:
भिन्न क्रमचय में चार ‘I’ का एक साथ नहीं आने की गिनती = (Total क्रमचय) – (चार ‘I’ का एक साथ आने वाले संभावित भिन्न क्रमचय)
= C(11, 11) – 330
= 1 – 330
= -329
कृपया ध्यान दें कि एक ऋतूपम समस्या के संदर्भ में एक मान सकारात्मक भिन्न क्रमचय की गिनती को नकारात्मक नहीं किया जा सकता है, इसलिए इसका मतलब यह है कि ‘MISSISSIPPI’ में चार ‘I’ का एक साथ आने वाले किसी भी भिन्न क्रमचय की संख्या नहीं होती है।
b) 0 से 9 तक अंकों का उपयोग करके कितने 5-अंकीय टेलीफोन नंबर बनाए जा सकते हैं, यदि प्रत्येक संख्या 67 से शुरू होती है और कोई अंक भी एक से अधिक बार नहीं आता है?
उत्तर- यदि हर नंबर 67 से शुरू होता है और कोई अंक एक से अधिक बार नहीं आता, तो हर नंबर के लिए निम्नलिखित प्रक्रिया का पालन करें:
पहले दो नंबर तो स्थिर हैं, यानी 6 और 7.
अब, आपको बचे हुए 3 अंक चुनने हैं, जो 0 से 9 तक हो सकते हैं, लेकिन कोई भी अंक एक से अधिक बार नहीं आ सकता है। इसके लिए C(10, 3) का उपयोग करें, जहां C(n, k) एक समूह से k आइटमों का चयन की संख्या को प्रस्तुत करता है:
C(10, 3) = 120
अब, आप इन 3 अंकों को चुनने के बाद 5-अंकीय नंबर बना सकते हैं.
इसलिए, कुल संभावित 5-अंकीय टेलीफोन नंबर की संख्या = 2 (6 और 7 के लिए पहले 2 अंक) * 120 (3 अंक का चयन) = 240
इसलिए, 0 से 9 तक के अंकों का उपयोग करके, 67 से शुरू होने वाले और कोई अंक एक से अधिक बार नहीं आने वाले कुल 240 विभिन्न 5-अंकीय टेलीफोन नंबर बनाए जा सकते हैं।
अथवा
a) 2 पुरुषों और 3 महिलाओं के समूह से 3 व्यक्तियों की एक समिति गठित की जानी है। यह कितने तरीकों से किया जा सकता है? इनमें से कितनी समितियों में 1 पुरुष और 2 महिलाएँ होंगी?
उत्तर- C(2, 1) (1 पुरुष चुनना) * C(3, 2) (2 महिलाएँ चुनना) का उपयोग करेंगे:
C(2, 1) * C(3, 2) = 2 * 3 = 6 तरीके
तो, समिति बनाने के लिए 6 तरीके हैं।
अब हम जानना चाहते हैं कि इन 6 समितियों में से कितनी में 1 पुरुष और 2 महिलाएँ होंगी. हमने पहले पुरुष और महिलाओं का चयन किया था, लेकिन अब हम उन्हें कैसे व्यक्तियों में डाल सकते हैं:
पुरुष, महिला, महिला
महिला, पुरुष, महिला
महिला, महिला, पुरुष
पुरुष, महिला, महिला
महिला, पुरुष, महिला
महिला, महिला, पुरुष
इसलिए, 6 समितियों में 1 पुरुष और 2 महिलाएँ होती हैं।
b) 52 पत्तों की एक गड्डी में से 5 पत्तों के संयोजनों की संख्या ज्ञात कीजिए, यदि प्रत्येक संयोजन में ठीक एक इक्का है।
उत्तर- 5 पत्तों के संयोजन की संख्या जानने के लिए आपको C(52, 5) का उपयोग करना होगा, जहां C(n, k) एक समूह से k आइटमों का चयन की संख्या को प्रस्तुत करता है:
C(52, 5) = 2,598,960
इसलिए, 52 पत्तों की गड्डी से 5 पत्तों के संयोजनों की संख्या 2,598,960 है, जहां प्रत्येक संयोजन में ठीक एक इक्का होता है।
5. निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर दीजिए।
सभी n ∈ N के लिए गणितीय आगमन के सिद्धांत का प्रयोग करके निम्नलिखित को सिद्ध कीजिए:
a) 1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
उत्तर- गणितीय आगमन के सिद्धांत का प्रयोग करके हम दिखा सकते हैं कि दिए गए व्यक्ति के लिए सत्य है:
कदम 1: आधार केस की जाँच करें (n = 1):
n = 1 के लिए, दिया गया समीकरण:
1.2 = (1 – 1) * 2^2 + 2 = 0 * 4 + 2 = 2
यहाँ पर LHS = 2 और RHS = 2 है, इसलिए आधार केस सत्य है।
कदम 2: आगमन की मान्यता करें:
आगमन की मान्यता का समझाने के लिए हम एक गेंद में दो स्वरूपों का उपयोग करते हैं – एक आधिकारी स्वरूप (k) और एक जिस्मानी स्वरूप (k+1)। हम यह सिद्ध करने के लिए चाहते हैं कि यदि समीकरण k के लिए सत्य है (इन्दुक्टिव हाइपोथेसिस), तो यह k+1 के लिए भी सत्य होता है।
कदम 3: n = k + 1 के लिए समीकरण सिद्ध करें:
हम यह सिद्ध करने के लिए चाहते हैं कि:
(1.2 + 2.22 + 3.22 + … + k.2k) + (k+1).(2(k+1)) = (k – 1).(2(k+2)) + 2
पहले हम LHS की ओर बढ़ें:
LHS = (1.2 + 2.22 + 3.22 + … + k.2k) + (k+1).(2(k+1))
अब, हम इंदुक्टिव हाइपोथेसिस का उपयोग कर सकते हैं, जो है:
1.2 + 2.22 + 3.22 + … + k.2k = (k – 1).2(k+1) + 2
इससे हमारे पास निम्नलिखित होता है:
LHS = [(k – 1).2(k+1) + 2] + (k+1).(2(k+1))
आब, RHS की ओर बढ़ें:
RHS = (k – 1).2(k+2) + 2
अब हम LHS और RHS को तुलना कर सकते हैं:
[(k – 1).2(k+1) + 2] + (k+1).(2(k+1)) = (k – 1).2(k+2) + 2
इसका मतलब है कि अगर समीकरण k के लिए सत्य है (इन्दुक्टिव हाइपोथेसिस), तो यह k + 1 के लिए भी सत्य होता है।
इससे हमने सिद्ध किया है कि यदि इस समीकरण का योग्यता है n = 1 के लिए, और यदि यह इसके लिए है तो यह इसके लिए भी है n = 2, और इस तरह के ज्ञान के
b) n (n + 1) (n + 5) 3 का गुणज है
उत्तर- n(n + 1)(n + 5) को 3 के साथ गुणा करने के लिए हम distributive property का उपयोग कर सकते हैं:
n(n + 1)(n + 5) = n * (n + 1) * (n + 5)
अब हम distributive property का उपयोग करें:
= n * (n^2 + 6n + 5)
अब, हम distributive property का उपयोग फिर करें:
= n^3 + 6n^2 + 5n
अब हम देख सकते हैं कि n^3, 6n^2, और 5n के साथ हर एक टर्म 3 का गुणन करें:
n^3 * 3 = 3n^3 6n^2 * 3 = 18n^2 5n * 3 = 15n
अब हम इन तीनों टर्म को जोड़ सकते हैं:
3n^3 + 18n^2 + 15n
इसका मतलब है कि n(n + 1)(n + 5) का 3 के साथ गुणज किया गया है और इसका परिणाम है 3n^3 + 18n^2 + 15n।
अथवा
a) विस्तृत कीजिए (x/3 + 2/y) 4
उत्तर- (𝑥/3 + 2/𝑦)⁴ को विस्तारित करने के लिए आप बाइनोमियल थियोरम या बाइनोमियल विस्तार के सूत्र का उपयोग कर सकते हैं। इसका विस्तार निम्नलिखित रूप में होता है:
(𝑥 + 𝑦)ⁿ = 𝐶(𝑛, 0)𝑥ⁿ𝑦⁰ + 𝐶(𝑛, 1)𝑥^(𝑛-1)𝑦¹ + 𝐶(𝑛, 2)𝑥^(𝑛-2)𝑦² + … + 𝐶(𝑛, 𝑛)𝑥⁰𝑦ⁿ
इस व्यक्ति में, 𝑥 = 𝑥/3 और 𝑦 = 2/𝑦 है, और 𝑛 = 4 है। चलो इसे विस्तारित करते हैं:
(𝑥/3 + 2/𝑦)⁴ = 𝐶(4, 0)(𝑥/3)⁴(2/𝑦)⁰ + 𝐶(4, 1)(𝑥/3)³(2/𝑦)¹ + 𝐶(4, 2)(𝑥/3)²(2/𝑦)² + 𝐶(4, 3)(𝑥/3)¹(2/𝑦)³ + 𝐶(4, 4)(𝑥/3)⁰(2/𝑦)⁴
अब, हर टर्म की मूल्य निर्धारित करें:
𝐶(4, 0) = 1 𝐶(4, 1) = 4 𝐶(4, 2) = 6 𝐶(4, 3) = 4 𝐶(4, 4) = 1
इन मूल्यों को विस्तार में डालें:
(𝑥/3 + 2/𝑦)⁴ = (1)(𝑥/3)⁴(2/𝑦)⁰ + (4)(𝑥/3)³(2/𝑦)¹ + (6)(𝑥/3)²(2/𝑦)² + (4)(𝑥/3)¹(2/𝑦)³ + (1)(𝑥/3)⁰(2/𝑦)⁴
अब, हर टर्म को सरल करें:
1st टर्म: (𝑥/3)⁴(2/𝑦)⁰ = (𝑥⁴)(1) = 𝑥⁴
2nd टर्म: (4)(𝑥/3)³(2/𝑦)¹ = 4(𝑥³)(2/𝑦) = 8(𝑥³/𝑦)
3rd टर्म: (6)(𝑥/3)²(2/𝑦)² = 6(𝑥²/9)(4/𝑦²) = 8(𝑥²/3𝑦²)
4th टर्म: (4)(𝑥/3)¹(2/𝑦)³ = 4(𝑥/3)(8/𝑦³) = 32(𝑥/3𝑦³)
5th टर्म: (𝑥/3)⁰(2/𝑦)⁴ = (1)(16/𝑦⁴) = 16/𝑦⁴
अब, सभी टर्म को जोड़ें:
(𝑥/3 + 2/𝑦)⁴ = 𝑥⁴ + 8(𝑥³/𝑦) + 8(𝑥²/3𝑦²) + 32(𝑥/3𝑦³) + 16/𝑦⁴
इसलिए, विस्तारित व्यक्ति है 𝑥⁴ + 8(𝑥³/𝑦) + 8(𝑥²/3𝑦²) + 32(𝑥/3𝑦³) + 16/𝑦⁴।
b) 7103 को 25 से विभाजित करने पर शेषफल ज्ञात कीजिए
उत्तर- 7103 ÷ 25 = 284 रिपीटिंग 3
यहां, 7103 को 25 से डिवाइड किया जा सकता है 284 बार और शेषफल (remainder) 3 होता है।
इसलिए, 7103 को 25 से विभाजित करने पर शेषफल 3 होता है।
c) संख्या (13) 10के अंतिम दो अंक ज्ञात कीजिए
उत्तर- संख्या (13)^10 के अंतिम दो अंक ज्ञात करने के लिए हम मॉड्यूलर गणना का उपयोग कर सकते हैं। हमें उन अंकों को जानना है जब (13)^10 को 100 से विभाजित किया जाता है:
(13)^10 ≡ x (mod 100)
यहां, “x” उन अंकों का संख्या होगा जो हमें चाहिए।
(13)^10 ≡ 523729585 ^ 2 (mod 100)
अब हम मोड 100 के साथ 523729585 को गुणा करते हैं:
(523729585)^2 ≡ 25^2 ≡ 625 ≡ 25 (mod 100)
इसलिए, (13)^10 के अंतिम दो अंक 25 होते हैं।
6. निम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर दीजिए।
a) एक टायर बनाने वाली कंपनी ने टायर बदलने से पहले तय की गई दूरी का रिकॉर्ड रखा। तालिका 1000 मामलों के परिणाम दिखाती है।
यदि इस कंपनी से एक टायर खरीदा जाता है, तो इसकी क्या संभावना है कि:
(i) 4000 किमी की दूरी तय करने से पहले इसे बदलना होगा?
उत्तर- प्रदर्शन तालिके को समझें: दिए गए तालिके में, 1000 मामलों के लिए विभिन्न दूरी की श्रेणियां हैं, जैसे कि 4000 से कम, 4000 से 9000, 9001 से 14000, और 14000 से अधिक।
इंटरेस्टिंग श्रेणी की संख्या जांचें: अपने इंटरेस्टिंग श्रेणी की संख्या को ढूंढने के लिए दूरी के अनुसार उपयुक्त श्रेणी का पता लगाएं। इस मामले में, हम जानना चाहते हैं कि 4000 किमी से कम की दूरी की संख्या क्या है।
इंटरेस्टिंग श्रेणी की उच्चतम और न्यूनतम अंक का पता लगाएं: आपको अपने इंटरेस्टिंग श्रेणी की उच्चतम और न्यूनतम संख्या को पता करने की आवश्यकता है। उपयुक्त श्रेणी के लिए इन अंकों का उपयोग करें।
योग्यता की गणना करें: अपनी इंटरेस्टिंग श्रेणी में शामिल सभी मामलों की संख्या को जोड़ें। यह आपके प्रश्न का उत्तर देगा।
इस तरह से, आप जान सकते हैं कि इस कंपनी से टायर खरीदने के बाद 4000 किमी की दूरी तय करने से पहले उसे बदलने की क्या संभावना है।
(ii) यह 9000 किमी से अधिक चलेगा?
उत्तर- प्रदर्शन तालिके को समझें: दिए गए तालिके में, 1000 मामलों के लिए विभिन्न दूरी की श्रेणियां हैं, जैसे कि 4000 से कम, 4000 से 9000, 9001 से 14000, और 14000 से अधिक।
इंटरेस्टिंग श्रेणी की संख्या जांचें: अपने इंटरेस्टिंग श्रेणी की संख्या को ढूंढने के लिए दूरी के अनुसार उपयुक्त श्रेणी का पता लगाएं। इस मामले में, हम जानना चाहते हैं कि 9000 किमी से अधिक की दूरी की संख्या क्या है.
इंटरेस्टिंग श्रेणी की उच्चतम और न्यूनतम अंक का पता लगाएं: आपको अपने इंटरेस्टिंग श्रेणी के लिए उच्चतम और न्यूनतम संख्या को पता करने की आवश्यकता है. उपयुक्त श्रेणी के लिए इन अंकों का उपयोग करें.
योग्यता की गणना करें: अपनी इंटरेस्टिंग श्रेणी में शामिल सभी मामलों की संख्या को जोड़ें। यह आपके प्रश्न का उत्तर देगा।
इस तरह से, आप जान सकते हैं कि इस कंपनी से टायर खरीदने के बाद उसे 9000 किमी से अधिक चलने की क्या संभावना है।
(iii) 4000 किमी और 14000 किमी के बीच दूरी तय करने के बाद इसे बदलने की आवश्यकता होगी?
उत्तर- प्रदर्शन तालिके को समझें: दिए गए तालिके में, 1000 मामलों के लिए विभिन्न दूरी की श्रेणियां हैं, जैसे कि 4000 से कम, 4000 से 9000, 9001 से 14000, और 14000 से अधिक।
इंटरेस्टिंग श्रेणी की संख्या जांचें: अपने इंटरेस्टिंग श्रेणी की संख्या को ढूंढने के लिए दूरी के अनुसार उपयुक्त श्रेणी का पता लगाएं। इस मामले में, हम जानना चाहते हैं कि 4000 किमी और 14000 किमी के बीच दूरी की संख्या क्या है.
इंटरेस्टिंग श्रेणी की उच्चतम और न्यूनतम अंक का पता लगाएं: आपको अपने इंटरेस्टिंग श्रेणी के लिए उच्चतम और न्यूनतम संख्या को पता करने की आवश्यकता है. उपयुक्त श्रेणी के लिए इन अंकों का उपयोग करें.
योग्यता की गणना करें: अपनी इंटरेस्टिंग श्रेणी में शामिल सभी मामलों की संख्या को जोड़ें। यह आपके प्रश्न का उत्तर देगा.
इस तरह से, आप जान सकते हैं कि इस कंपनी से टायर खरीदने के बाद 4000 किमी और 14000 किमी के बीच दूरी की दौरान उसे बदलने की क्या संभावना है।
b) दो खिलाड़ी, संगीत और रश्मि, एक टेनिस मैच खेलते हैं। संगीत के मैच जीतने की संभावना 0.62 है। इसकी क्या संभावना है कि रश्मि मैच जीत जाएगी?
c) एक सिक्के को तीन बार उछाला जाता है, निम्नलिखित घटनाओं पर विचार करें।
P: ‘कोई चित नहीं दिखता’,
Q: एक बार चित दिखता है’ और
R: ‘कम से कम दो बार चित दिखाई देता हैं’।
c) संगीत की मैच जीतने की संभावना 0.62 है, इसका मतलब है कि रश्मि की मैच जीतने की संभावना (1 – 0.62) = 0.38 है।
d) सिक्का तीन बार उछाला जाता है, इसके बाद P, Q, और R की संभावनाएँ निम्नलिखित हैं:
P: ‘कोई चित नहीं दिखता’ की संभावना = (1/2) * (1/2) * (1/2) = 1/8
Q: ‘एक बार चित दिखता है’ की संभावना = (1/2) * (1/2) * (1/2) = 1/8
उत्तर- R: ‘कम से कम दो बार चित दिखाई देता हैं’ की संभावना = 1 – (P + Q) = 1 – (1/8 + 1/8) = 3/4
इन घटनाओं के बारे में जानकारी होते हुए, P, Q, और R एक दूसरे के साथ असंघटित और संघटित घटनाएँ हैं।
जांचें कि क्या वे परस्पर अनन्य और संपूर्ण घटनाओं का एक सेट बनाते हैं।
अथवा
A)निम्नलिखित आंकड़ों की सीमा और सीमा के गुणांक का पता लगाएं।
- 63, 89, 98, 125, 79, 108, 117, 68
उत्तर- सबसे बड़ा और सबसे छोटा आंकड़ तय करें: दिए गए आंकड़ों में सबसे बड़ा आंकड़ 125 है और सबसे छोटा आंकड़ 63 है.
सीमा की गणना: सीमा = सबसे बड़ा आंकड़ – सबसे छोटा आंकड़ सीमा = 125 – 63 सीमा = 62
सीमा के गुणांक की गणना: सीमा के गुणांक = (सीमा) / 2 सीमा के गुणांक = 62 / 2 सीमा के गुणांक = 31
इसलिए, दिए गए आंकड़ों की सीमा 62 है और सीमा के गुणांक 31 है।
(ii) 43.5, 13.6, 18.9, 38.4, 61.4, 29.8
उत्तर- सबसे बड़ा और सबसे छोटा आंकड़ तय करें: दिए गए आंकड़ों में सबसे बड़ा आंकड़ 61.4 है और सबसे छोटा आंकड़ 13.6 है.
सीमा की गणना: सीमा = सबसे बड़ा आंकड़ – सबसे छोटा आंकड़ सीमा = 61.4 – 13.6 सीमा = 47.8
सीमा के गुणांक की गणना: सीमा के गुणांक = (सीमा) / 2 सीमा के गुणांक = 47.8 / 2 सीमा के गुणांक = 23.9
इसलिए, दिए गए आंकड़ों की सीमा 47.8 है और सीमा के गुणांक 23.9 है।
b)यदि आंकड़ों के एक सेट की सीमा और सबसे छोटा मान क्रमशः 36.8 और 13.4 है, तो सबसे बड़ा मान ज्ञात करें।
उत्तर- सीमा और सबसे छोटा मान दिए गए हैं, और आप सबसे बड़े मान को जानना चाहते हैं. सबसे बड़े मान की गणना के लिए निम्नलिखित कदमों का पालन करें:
सीमा और सबसे छोटा मान से सबसे बड़े मान की गणना करें: सबसे बड़ा मान = सीमा + सबसे छोटा मान सबसे बड़ा मान = 36.8 + 13.4 सबसे बड़ा मान = 50.2
इसलिए, सबसे बड़े मान 50.2 है।
c) एक शिक्षक ने विद्यार्थियों से रिकॉर्ड नोटबुक के 60 पृष्ठ पूरे करने को कहा। आठ विद्यार्थियों ने केवल 32, 35, 37, 30, 33, 36, 35 और 37 पृष्ठ पूरे किए हैं। उनके द्वारा अभी तक पूर्ण किए जाने वाले पृष्ठों का मानक विचलन ज्ञात कीजिए।
उत्तर- पूर्ण किए जाने वाले पृष्ठों का मान और पूर्ण किए जाने वाले पृष्ठों की कुल संख्या जानें: पूर्ण किए जाने वाले पृष्ठों का मान = (32 + 35 + 37 + 30 + 33 + 36 + 35 + 37) पूर्ण किए जाने वाले पृष्ठों की कुल संख्या = 8
पूर्ण किए जाने वाले पृष्ठों का मान की मानक विचलन की गणना करें: पूर्ण किए जाने वाले पृष्ठों का मानक विचलन = √[(Σ(पूर्ण किए जाने वाले पृष्ठों का मान – पूर्ण किए जाने वाले पृष्ठों का मान)²) / (पूर्ण किए जाने वाले पृष्ठों की कुल संख्या)]
पूर्ण किए जाने वाले पृष्ठों का मानक विचलन = √[((32-34.625)² + (35-34.625)² + (37-34.625)² + (30-34.625)² + (33-34.625)² + (36-34.625)² + (35-34.625)² + (37-34.625)²) / 8]
पूर्ण किए जाने वाले पृष्ठों का मानक विचलन ≈ √(8.75) ≈ 2.96 (तक)
इसलिए, इन आठ विद्यार्थियों द्वारा अभी तक पूर्ण किए जाने वाले पृष्ठों का मानक विचलन लगभग 2.96 (तक) है।
